Q.C.M. Probabilité
Plusieurs bonnes réponses sont possibles.
Exercice 1
Exercice 2
Exercice 3
Dans un groupe 75% des gens aiment les pommes, 60% les poires et 40% n'aiment que les pommes.
Compléter le tableau, A représente aimer les pommes et B aimer les poires. On mettre les nombres en % sans utiliser le symbole %.
Exercice 4
Exercice 5
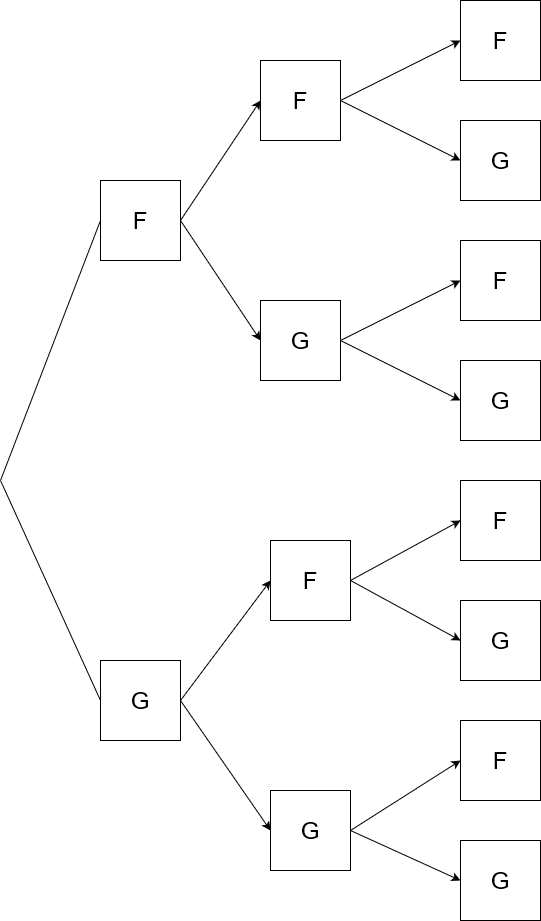
On prend une famille de trois enfants, on se pose la question de savoir si les enfants sont des garçons ou des filles, l'arbre est ci dessous :