Algorithmes

Définition

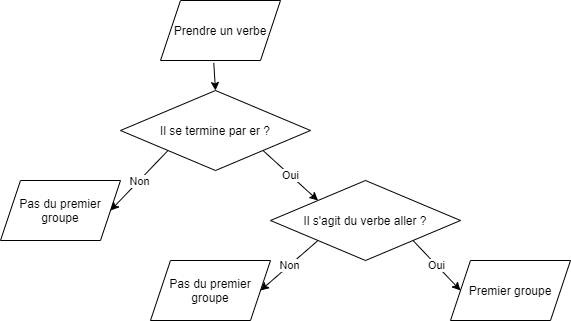
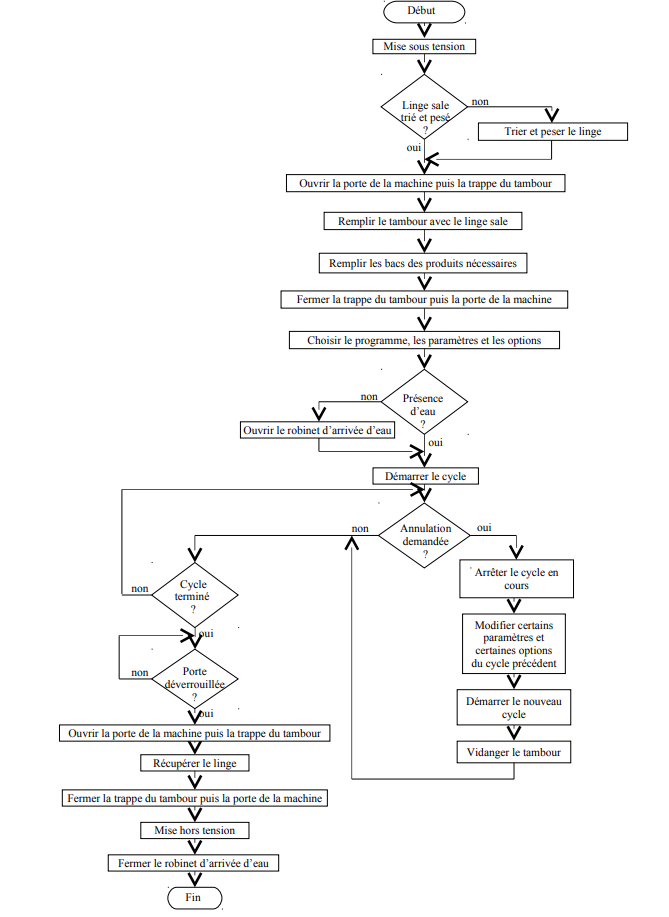
Un algorithme est une liste précise d’étapes à suivre permettant de résoudre un problème.

Par exemple :

• Un algorithme permettant de savoir si un verbe est du premier groupe :

• Un algorithme pour le fonctionnement d'une machine à laver.

• L'algorithme d'Euclide.

Il existait des algorithmes bien avant la naissance des ordinateurs, vous en utilisez sans vous en rendre compte par exemple si vous suivez une recette de cuisine, vous utilisez une machine à café...

Les ordinateurs vont néanmoins marquer une révolution au niveau des algorithmes calculatoires, qui iront beaucoup-beaucoup plus vite.

Actuellement il existe des algorithmes qui demandent trop de calculs même aux ordinateurs les plus puissants.

On arrive aussi à montrer que toutes choses ne peut pas être résolu via un algorithme, par exemple il n'est pas possible d'avoir un anti-virus parfait ou encore on peut pas tout compresser.

Nous allons décrire un algorithme dans le style de programmation de python.

Les variables

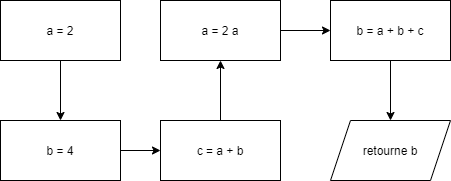
Une des façons de décrire un algorithme est d’utiliser des variables, ces variables vont contenir des nombres (ou des mots…) et vont changer en cours de route. Quand on veut affecter une variable (a par exemple) le nombre 10 on écrit : a = 10.

Attention l'égalité veut dire affectation et n'a pas le même sens qu'en mathématiques, en maths x à une valeur qui ne change pas en cours de route. Ce qui n'est pas le cas en informatique.

Les conditions

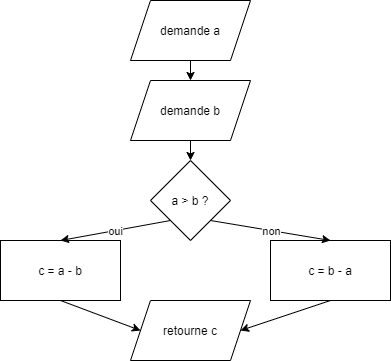
Les conditions sont des parties très importantes d’un algorithme. Elle permettent de gérer différents situations possibles.

Logique

La logique est partie qui peut vite devenir dure des mathématiques, pour simplifier on va considérer qu'une proposition peut être Vraie ou Fausse et on définit trois fonctions ET OU et NON sur les propositions :

• P1 ET P2 est vraie si P1 et P2 ensemble sont vraies sinon P1 et P2 et faux.
• P1 OU P2 est vraie si soit P1 soit P2 soit les deux ensembles sont vraies sinon P1 OU P2 et faux.
• NON P1 est vraie si P1 est faux et faux si P1 est vraie.

Instruction si

L'instruction si ou if en anglais permet de séparer les calculs.

Les boucles

Tant que

On peut répéter une partie d’un algorithme (on dit faire une boucle) tant qu’une certaine condition n’est pas vérifiée.

Instruction	a	b	r
Demande a	10
Demande b	10	8
Calcule r	10	8	2
r = 0 ?	10	8	2
a = b	8	8	2
b = r	8	2	2
Calcule r	8	2	0
r = 0 ?	8	2	0
Affiche b

For

Si la boucle tant que est suffisante on utilise aussi une boucle for quand on sait à l’avance combien de fois la boucle va se répéter.

Saisir a
Saisir b
s = 0
Pour i allant de 1 à b répéter :
	s = s + a
Fin pour
affiche s