Algorithme d'apprentissage.

Deux étapes symboliques de l'intelligence artificielle.

Deep Blue contre Kasparov

En 1997 IBM grace à son super ordinateur Deep Blue bat le champion d'échec de l'époque Garry Kasparov.

L'algorithme de Deep blue était basé sur la force brute, l'ordinateur examine tous les prochains coups successifs possibles et choisi la meilleure possibilité pour lui.

Un problème est la complexité de l'algorithme, la force brute est exponentielle par rapport au nombre de coups successifs (si on le programme pour un puissance 4 par exemple l'algorithme est en \(\Theta(7^n)\) et donc rapidement la puissance de l'ordinateur sera insuffisante et il est donc impossible d'aller jusqu’à la fin du jeu et doit doit s’arrêter à 7-8 coups à l'avance si on veut un temps de calcul raisonnable.

Pour cette méthode il faut aussi une fonction d'évaluation d'une position, qui doit être faite par un expert du jeu. Cette fonction est nécessaire pour savoir justement quelle position est la meilleure.

A cette époque un jeu résistait à la force brute : le go, et à l'époque on pensait que jamais un ordinateur battrait (un bon) joueur humain.

Alpha go contre Lee Sedol

En 2016, le programme alphago (appartenant à Google) bat Lee Sedol un des meilleurs joueurs de go au monde:

Le programme ne se repose plus uniquement sur la force brute, il utilise aussi des techniques d'apprentissages.

L’algorithme des k plus proches voisins.

Présentation

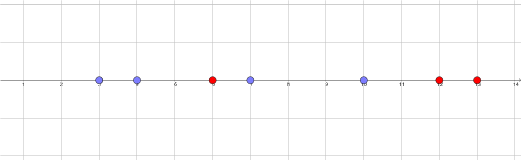
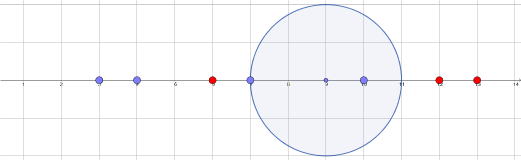
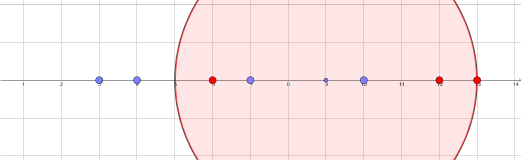
L'algorithme des plus plus proches voisins est un algorithme de prédiction, par exemple :

• On donne une photo, et l'ordinateur va dire si c'est un chat ou un chien.
• On donne les dimension d'une fleur et l'ordinateur va donner sa nature.
• On donne une écriture manuscrite et l'ordinateur va lire les caractères.
• L'ordinateur analyse vos recherches et va vous fournir les publicités qui vont vous interresser.

Le principe de l'algorithme est assez simple et on va le décrire dans le cas de points :

• On donne liste d'exemple à l'ordinateur, ici des points rouges ou bleu sur une droite :

• On considère un nouveau point à l'abscisse 9, et on se pose la question de savoir si il est rouge ou bleu :
• Si k = 2, les deux plus proches voisins sont les points d'abscisses 7 et 10, ils sont bleus et l'algorithme des 2 plus proches voisins prédit que le nouveau point est bleu.

• Si k = 5, les cinq plus proches voisins sont deux bleus et trois rouges, l'algorithme des 5 plus proches voisins prédit que le nouveau point est rouge.

Un cas concret : Les iris.

L'iris est une fleur qui a au moins trois variétés :

On récupére 150 données sur la longueur et la largeur des pétales des fleurs. Sur la représentation graphique de ses données on constate trois groupes distincts. l'algorithme knn essaye de remplacer l'oeil humain pour savoir dans quel groupe on se trouve.

Généralement on divise la base des données en deux, une partie des données va servir à "apprendre" et l'autre à tester pour savoir si notre distance ou si le choix de k est pertinant.

Autre exemple : Reconnaître des symboles.

Dans un premier temps, entrez différents exemples de trois symboles. Ensuite entrer une des trois formes et lancez le bouton correspondance, il lancera l'algorithme des k plus proches voisins pour essayer de trouver quel symbole vous avez essayé de dessiner.

La distance utilisée ici effectue la racine de la somme des différences au carré pour chaque pixel de l'image 1 et du même pixel de l'image 2. Pour simplifier, si l'image est constituée de 4 pixels ou noirs (codé à 1) ou blancs (codé à 0) alors la distance entre les deux images ci dessous est :

est égale à \(\sqrt{(0-0)²+(1-1)²+(1-1)²+(0-1)²} = 1\)

Le deep learning - Les réseaux de neurones

Le deep learning utilise une technique très différente d'apprentissage basée sur un réseau de neurones, donnons le principe très simplifié pour l'ewemple suivant, en entrée et en sortie nous avons deux bits, nous souhaitons que le réseau apprenne la fonction suivante :

Partons d'un réseau de neurone suivant (les nombres sont générerer aléatoirement au début):

Il faut maintenant faire "apprendre", l'opération consiste à donner des entrées, à voir les sorties obtenus par le réseau et à les comparer avec les vraies sorties.

Si on donne l'entrée E₁ = 1 et E₂ = 0 alors on obtient :

Là on calcule les erreurs en comparant avec les bonnes réponses et on fait deux choses :

1. on répercute les erreurs de facon proportionnelle, par exemple neurone S₁ dit être à 1 et pas à 0.19 on a donc une erreur de -0.81, cette erreur vient au 3/4 (0.3/(0.3+0.1)) de N₁ et au 1/4 de N₂ donc l'erreur sur S₁ va donner une erreur de -0.60075 sur N₁ et de -0.2025 sur N₂ on ajoute ensuite l'erreur qui vient de S₂.

   

2. On modifie les coefficients entre les neurones en utilisant une formule mathématique qui généralise la notion dérivation vu en cours de mathématiques (on parle de gradient). Cette opération est compliquée car il ne faut pas modifier trop rapidement les coefficients. Les modifications ci dessous sont totalement fictive mais donne l'idée.

   

Pour aboutir à un réseau performant il faut beaucoup l’entraîner et cela demande énormément de temps de calcul, heureusement cette opération est parallélisable dans l'ordinateur. Dans l'exemple ci dessous qui correspond aux problèmes des Iris j'utilise un réseau de 6 × 3 neurones (comment choisir la bonne taille ? je ne sais pas).

Le problème vient de l’entraînement, mon jeu de données sur les fleurs est bien trop petits (si bien que je triche en ré entraînant avec les mêmes valeurs, ce qui fausse la chose).

Pour avoir un exemple plus parlant je divise le plan repéré euclidien en trois parties, la première des points M tels que OM < 1, le deuxième des OM < 2 et l reste. Comme ça je peux entraîner facilement :

Essayer de dessiner des zones de couleurs.

Definir le nombre de neurones par couche.